Tales de Mileto fue uno de los grandes filósofos de la Antigua Grecia, pero también fue un gran matemático al que se le atribuyen varias teorías que con el tiempo se han establecido en la base matemática. Una de ellas es la que se conoce propiamente como teorema de tales que suele aplicarse por ejemplo para calcular la altura de los edificios y que os explicamos a continuación al detalle, el Teorema de Tales: cómo se calcula, fórmula y para qué sirve.
Teorema de Tales: cómo se calcula, fórmula y para qué sirve
En realidad, dos son las teorías que reciben el nombre de Teorema de Tales por lo que iremos por partes para enunciarlos ambos y explicarlos bien dado que tiene relación.
Lo primero que debemos tener claro antes de empezar es la existencia de los llamados triángulos semejantes. Es decir, triángulos de la misma forma, con ángulos iguales y lados proporcionales pero que tienen distinto tamaño.
Por otro lado, tengamos también en cuenta las líneas paralelas, que mantienen la misma distancia pero que nunca se cruzan.
Primer teorema de Tales
A partir de lo mencionado, el primer teorema de tales establece que:
«Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado».
La fórmula de este teorema sería la siguiente:
![]()
En la imagen que veis a continuación, podéis ver cómo se aplica el teorema. A la derecha tenemos el triángulo cuyos lados son A, B y C. Si dibujamos dos líneas paralelas, obtenemos el triángulo semejante de la izquierda A´, B´ y C.
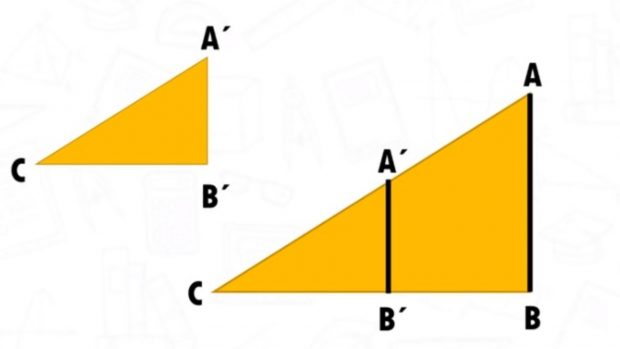
Segundo teorema de Tales
El segundo teorema hace referencia a las rectas paralelas enunciando lo siguiente:
«Si dos rectas cualesquiera se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.»
Esta es la fórmula que representa ese teorema:
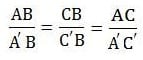
Aplicaciones del teorema de Tales
Ya hemos visto qué es y cómo se calcula el teorema de Tales pero si le buscamos aplicación en la vida real, tenemos que decir principalmente se utiliza para hacer el cálculo de lo que miden los edificios, tomando otro elemento como referencia. Así, se puede medir la altura de un bloque de pisos, tomando como referencia un árbol y teniendo además en cuenta los rayos del sol y la sombra del edificio de modo que si se dibuja un triángulo entre el edificio y la sombra, tomando como referente la altura del árbol nos aparecerá un triángulo semejante que determinará lo que mide el edificio.
Este es además uno de los teoremas más utilizados para hacer cálculos en trigonometría, en aquellos problemas en los que hay dos líneas paralelas.
