Las matemáticas cuentan con múltiples problemas que llevan años abiertos. Algunos se resisten y cada pequeño avance es celebrado en la comunidad como un paso que acerca a su resolución, habitualmente compleja. Otros están ahí, esperando que llegue la persona que los mire desde una nueva perspectiva que haga que, de pronto, todos los velos caigan y uno quede sorprendido ante la simplicidad de la solución.
Este es el caso de Lisa Piccirillo, que resolvió un importante problema en teoría de nudos, abierto hace más de 50 años, siendo estudiante de doctorado en la Universidad de Texas en Austin. Su resultado, que recientemente ha sido publicado en la prestigiosa revista Annals of Mathematics, ha despertado un gran interés en la comunidad matemática.
El entusiasmo de esta acogida ha sorprendido a la propia joven, que reconoce no haber sido consciente en un primer momento del impacto que tendría su trabajo.
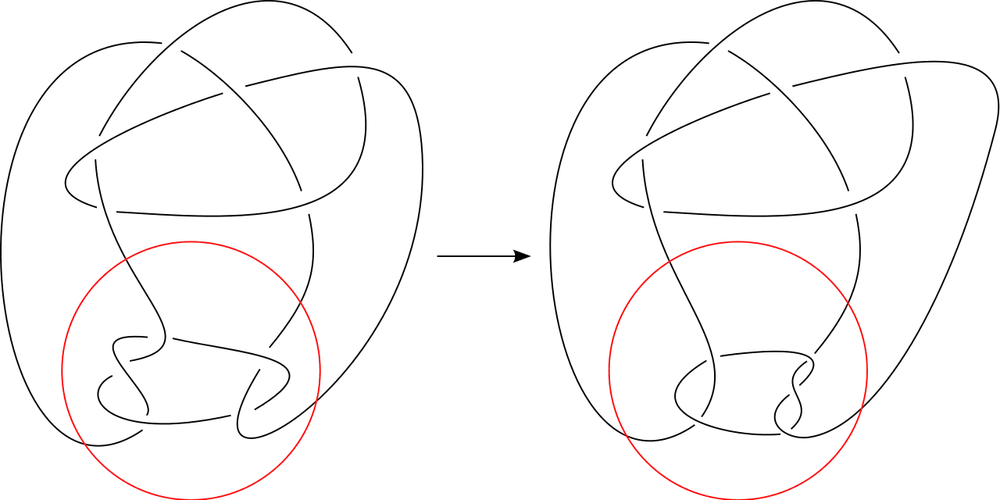
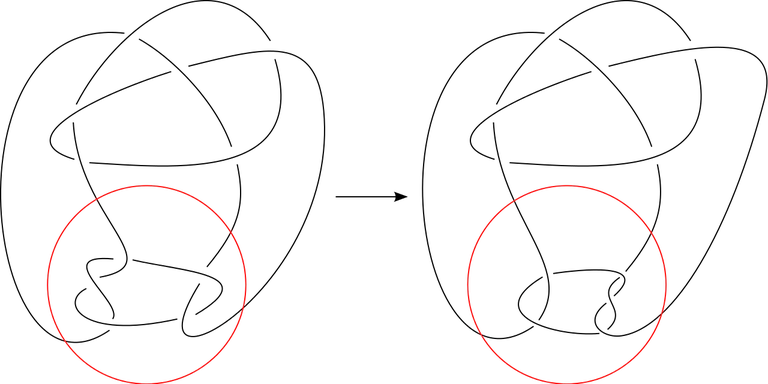
Piccirillo ha determinado que el llamado nudo de Conway, introducido por John Horton Conway (recientemente fallecido a causa de la Covid19), no tiene la propiedad de ser slice.
La pregunta fundamental que se intenta responder es si, dados dos nudos, es posible obtener uno de ellos a partir de deformaciones del otro. En caso de que sea posible, los nudos son equivalentes
Pero empecemos por el principio: en matemáticas, un nudo sería una cuerda atada en la se han pegado los extremos entre sí. La teoría de nudos estudia las transformaciones que pueden hacerse a esa cuerda estirándola, retorciéndola, doblándola… sin llegar a cortarla. La pregunta fundamental que se intenta responder es si, dados dos nudos, es posible obtener uno de ellos a partir de deformaciones del otro. En caso de que sea posible, los nudos son equivalentes.
Para resolver estas cuestiones se emplean los invariantes de nudos, que son funciones que asignan un valor a cada nudo. Si un determinado invariante asigna valores diferentes a dos nudos, entonces no es posible deformar un nudo en el otro, es decir, no son nudos equivalentes.
Los invariantes permiten estudiar las propiedades de los nudos. El problema resuelto por Piccirillo se centra en la propiedad de un nudo de ser slice. Para definir este concepto tenemos que imaginar el nudo en un espacio de cuatro dimensiones. Así, un nudo es slice si es el borde de un disco en este espacio. No es sencillo formarse una idea intuitiva y precisamente por esto no es fácil determinar, en general, si un nudo es slice o no.
Afortunadamente, los invariantes pueden ser útiles en esta tarea, ya que proporcionan obstrucciones para que un nudo sea slice. Así, hasta el momento había sido posible determinar si 2977 de los 2978 nudos con menos de 13 cruces tienen la propiedad de ser slice o no. Todos menos un nudo: el nudo de Conway, de 11 cruces.
Piccirillo supo de la existencia de este problema durante un congreso en el verano de 2018. En sus propias palabras, lo tomó como un pasatiempo
Piccirillo supo de la existencia de este problema durante un congreso en el verano de 2018. En sus propias palabras, lo tomó como un pasatiempo en el que aplicar algunas de las técnicas que había desarrollado como estudiante de doctorado. En poco menos de una semana consiguió dar respuesta a la pregunta: el nudo de Conway no es slice.
La prueba de su resultado es sorprendente por la combinación de originalidad y simplicidad (¡ojo con no confundir simplicidad con sencillez!). Su éxito radica en el uso de un invariante moderno para atacar un problema clásico: el “invariante s”, definido en 2010 por Jacob Rasmussen a partir de otro invariante conocido como homología de Khovanov, y en la idea de traza, un espacio de dimensión cuatro que puede asociarse a cada nudo. Si dos nudos tienen trazas equivalentes entonces o bien ambos tienen la propiedad de ser slice, o bien ninguno de los dos la tiene. La idea de Piccirillo consiste en construir un nudo cuya traza es equivalente a la traza del nudo de Conway, y usar el invariante s para comprobar que el primero no es slice.
Más allá de completar la clasificación de nudos slice de menos de 13 cruces, la importancia de este resultado se esconde en algo más sutil: en el estudio de la clasificación de nudos, es fundamental determinar qué propiedades se preservan por mutación. El nudo de Conway es mutante de otro nudo con nombre propio: el nudo de Kinoshita-Terasaka (ver Figura al margen), que sí es slice. Así, el trabajo de Piccirillo proporciona el primer ejemplo de un nudo no slice (que sí es topológicamente slice) cuyo mutante sí lo es.
Marithania Silvero es profesora ayudante, doctora de la Universidad de Huelva y miembro del Instituto de Matemáticas de la Universidad de Sevilla (IMUS).
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Edición y coordinación: Ágata A. Timón García-Longoria (ICMAT)
Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter