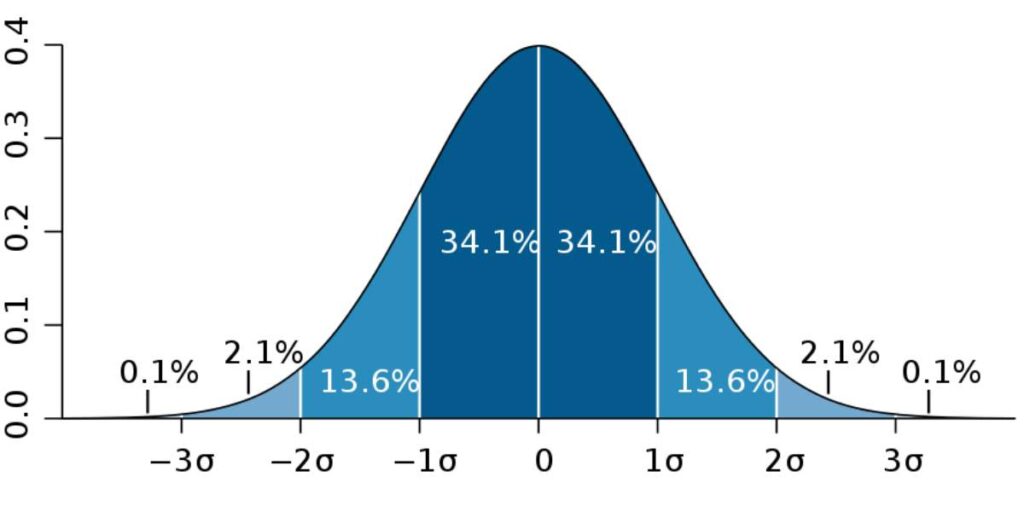
Seguramente, en algún momento durante tu paso por el colegio tuviste algún profesor que te enseñó lo que era la desviación típica en la clase de matemáticas e incluso puede que lo hayas visto en alguna asignatura de estadística, ¿Descubrimos qué es y cómo se calcula?
Es muy posible es que, cómo tantas cosas que aprendiste durante tu etapa escolar y que has olvidado, a día de hoy y con el paso del tiempo, ya no lo recuerdes. Y es que lo cierto ¡es que es algo de lo más normal y más común de lo que parece!
También es posible que te suene el concepto pero, que si alguien te pidiera calcularlo, no supieras por donde empezar, porque lo más seguro es que no estés muy familiarizado con la desviación típica ya que efectivamente no es algo que debamos usar todos los días. Sea cual sea tu caso pero, no debes preocuparte porque a continuación te contamos todo lo que necesitas saber para refrescar tu memoria y poder volver a calcular esta métrica siempre que lo necesites.
¿Qué es exactamente la desviación típica?
Pues no es otra cosa que la medida de dispersión que se usa en estadística cuando necesitamos obtener los resultados relativos tanto para variables cuantitativas como para variables de intervalo que sean lo más aproximados posibles a la población o, en otras palabras, la raíz cuadrada de la varianza de la variable.
Si quieres entenderla bien, es importante que sepas que te será de gran ayuda comprender primero otros conceptos como la desviación estándar y la varianza, así familiarízate primero con ellos antes de intentar calcular la desviación típica sin ningún referente.
Cuando lo hayas hecho, hacer los cálculos relativos a la raíz cuadrada te será mucho más sencillo y podrás por fin conocer la desviación que presentan los datos en su distribución respecto a la media aritmética de dicha distribución, que es el objetivo último de esta medida de dispersión.
En conclusión, la desviación típica lo que nos permite es tener una visión más acorde con la realidad en el momento de tomar las decisiones y esto es de lo más interesante y útil no solo para poder hacer predicciones que afecten al futuro de un negocio (y en consecuencia a la cantidad de dinero que se invierte en una acción concreta y que con esta podremos ganar).
También para conocer mejor las tendencias más repetidas en un cierto grupo de la población como qué programa de televisión es el más visto o cuál es el numero de hermanos más común que tienen las personas ¡e incluso para calcular la probabilidad que existe de obtener un resultado concreto en una tirada de dados!
Algunos detalles que debes saber antes de empezar a hacer el cálculo
Para identificarla en cualquier contexto algo que debes tener en cuenta es que qeneralmente siempre la encontrarás representada como σ, y que existen algunas propiedades de las que debemos ser conscientes, como el hecho que si a todos los valores de la variable se les suma un número la desviación típica no varía y que esta siempre será un valor positivo o cero en el caso de que las puntuaciones sean iguales.
Ten también en cuenta que si todos los valores de la variable se multiplican por un número la desviación típica quedará multiplicada por dicho número, y por último, que si tienes varias distribuciones con la misma media y conocemos sus respectivas desviaciones, con ello ya podrás calcular la desviación típica total.
¿Cuál es la forma correcta de calcular la desviación típica?
Aunque gracias a Internet hoy en día tenemos múltiples herramientas a nuestro alcance que nos permiten resolver ciertas preguntas matemáticas con solo introducir algunos datos en un sistema que calcula el dato específico que necesitemos, nunca está de más saber cómo calcular la desviación típica de forma manual para que no tener conexión a Internet no sea un problema; es por ello que, a continuación, te explicamos como hacerlo.
Lo primero que debemos hacer para poder calcular la desviación típica de la manera correcta es calcular la media de los datos, así que si por ejemplo hay dos personas, uno que mide 1,50 y otro que mide 1,60, la media será 1,55, que es el punto medio entre los dos ¡aunque ten en cuenta que puede ser que en algún caso no tengas datos reales sino intervalos! Pero también puedes descubrir la desviación típica con ellos.
Una vez sabemos la media, debemos calcular la varianza, sumando la marca de clase y restándole a esta la media de los datos al cuadrado por el número de datos que se corresponden por cada dato (f sub i) partido del número de datos que se cogen (n).
Así que debemos ir restando a la marca de clase, la media que hemos calculado antes y una vez que la tengamos, haremos el cuadrado y multiplicaremos cada uno por cada frecuencia de cada dato para sumarlo todo al final y por último dividirlo entre el número de datos que hay.
Recuerda que en este punto, para obtener la desviación típica ya solo necesitarás calcular la raíz de la varianza ¡y listo!
Ya solo debes ser consciente de que una desviación baja indicará que la mayoría de los datos se acumulan en torno a la media aritmética, pero sin embargo, obtener una desviación típica alta significará que hay mucha dispersión en nuestros datos y que los valores son muy extremos.