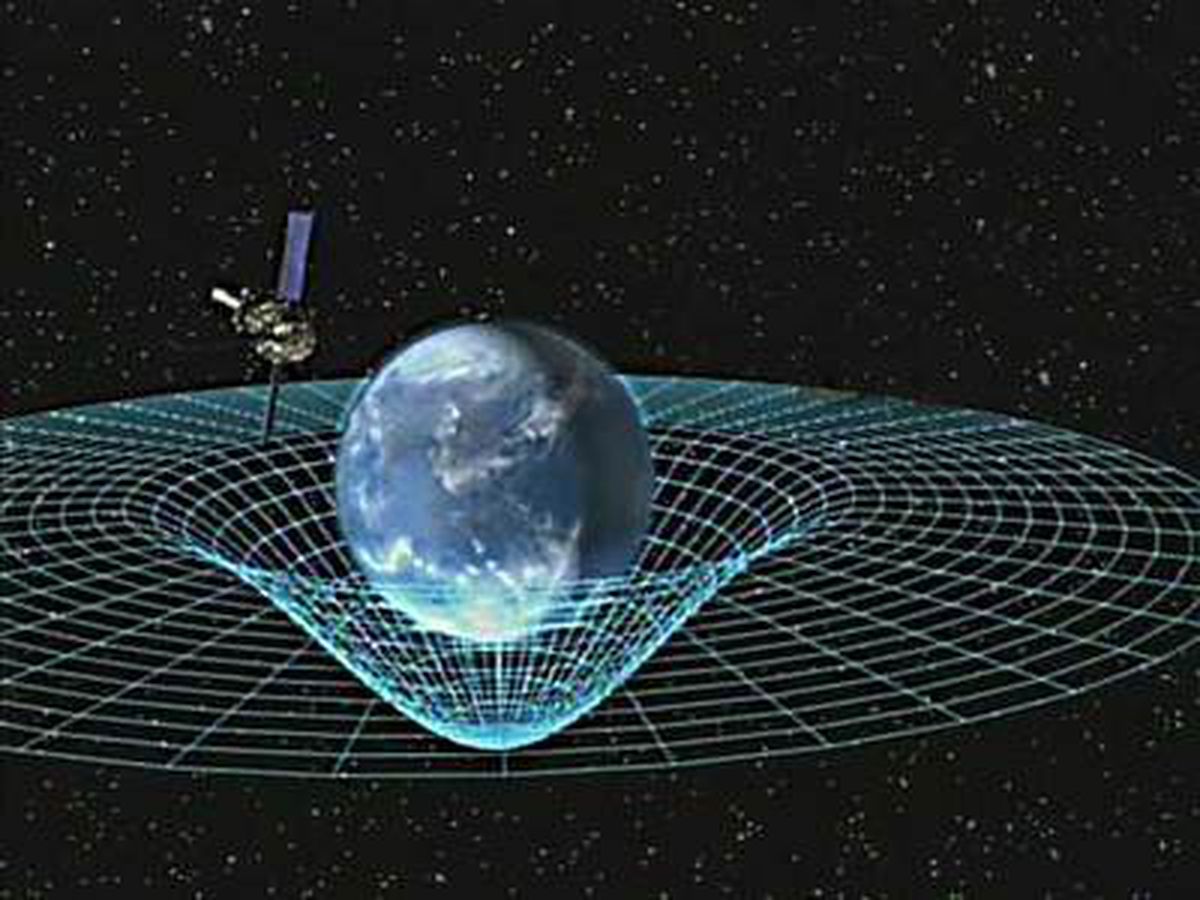
Una de las ideas más cautivadoras de la teoría de la relatividad general de Albert Einstein es que la luz viaja a velocidad constante, describiendo trayectorias que minimizan la distancia entre puntos. Más sorprendente todavía es la conclusión de que el espacio y el tiempo deben curvarse para acomodar este fenómeno. ¿Qué significa esto? ¿Cómo son los espacios curvados? ¿Qué es la curvatura, y cómo se mide?
Dar una definición precisa de qué es la curvatura requiere de conceptos matemáticos avanzados, pero podemos describir la curvatura de manera cualitativa en algunas situaciones. Por ejemplo, cuando el espacio en cuestión es igual para todos los observadores (es decir, es homogéneo) y tiene la misma pinta en todas las direcciones (isotrópico). Aunque esto no es cierto de manera local para nuestro universo —el Sistema Solar es muy diferente de una región vacía—, el principio cosmológico afirma que estas propiedades se satisfacen a gran escala.
En estos espacios, la curvatura se mide por el defecto angular de triángulos. Si tenemos tres puntos en el espacio, que conectamos por los caminos más cortos entre ellos (ojo, estos pueden no ser líneas rectas, como ocurre en el caso de una esfera), se obtiene un triángulo con vértices en esos puntos. Para obtener el defecto angular calculamos la suma de los ángulos del triángulo y restamos 180º. El resultado (que puede ser positivo, negativo o cero) es proporcional al área del triángulo, y el cociente del defecto angular por el área es precisamente la curvatura del espacio.
Si la curvatura es cero, nos encontramos con la geometría euclídea que estudiamos en la escuela, donde todos los triángulos tienen ángulos que suman 180º. A este tipo de espacios los llamamos espacios planos. Cuando la curvatura es positiva, los triángulos son más gordos que los triángulos euclídeos, como los que uno dibuja en una esfera. Por esta razón, este tipo de espacios se llaman esféricos; por supuesto, una esfera es un ejemplo de ellos. Finalmente, si la curvatura toma valores negativos , el triángulo es más fino que un triángulo euclídeo, como el que dibujaríamos en la superficie de una silla de montar, que recibe el nombre de paraboloide hiperbólico. Por esta razón, este tipo de espacios se llaman espacios hiperbólicos. Dar ejemplos de espacios hiperbólicos es más complicado, aunque podemos mencionar la pseudoesfera, que es la superficie que resulta de rotar la curva llamada tractriz a lo largo de una recta.
La mayor parte de la evidencia experimental (basada en el análisis de la radiación de fondo) sugiere que el universo es plano a gran escala, con un margen de error razonablemente pequeño.
Visualizar la curvatura es más sencillo cuando observamos superficies —objetos de dos dimensiones— dentro del espacio tridimensional. En este caso, la curvatura mide cómo y cuánto, la superficie se retuerce en el espacio
Visualizar la curvatura es más sencillo cuando observamos superficies —objetos de dos dimensiones— dentro del espacio tridimensional. En este caso, la curvatura mide cómo y cuánto, la superficie se retuerce en el espacio. De manera más concreta, si la superficie tiene curvatura positiva, cada uno de sus puntos parece una cúpula; si la curvatura es cero, entonces la superficie parece una línea recta en al menos una dirección, como en el caso de un plano o un cilindro; finalmente, todo punto de una superficie de curvatura negativa es un punto de silla: cerca del punto, la superficie se curva “hacia arriba” en una dirección, y “hacia abajo” en otra, como ocurre cerca de los bordes de una hoja de kale.
En general, una superficie puede tener puntos de curvatura positiva, negativa y nula, como ocurre con la superficie de un dónut. Si imaginamos esta superficie apoyada en el suelo, los puntos del círculo interior tienen curvatura negativa; los del círculo exterior, curvatura positiva; y los de los círculos superior e inferior, curvatura cero.
Por supuesto, ser capaz de observar un objeto desde fuera ofrece un punto de vista inmejorable para describir su forma. En esta situación, la curvatura hace referencia a una cualidad extrínseca de la superficie, que describe su forma en función del espacio que la rodea. No podemos disponer de este punto de vista en el caso de nuestro universo, ya que no hay nada fuera de él. De esta manera, la curvatura se convierte en una cualidad intrínseca y ofrece información sobre la forma del espacio tal y como sería percibida por una persona que viviera en él, sin ningún conocimiento de un espacio exterior, como ocurre con el defecto angular.
El hecho de que ambos puntos de vista coinciden fue demostrado por uno de los padres de la geometría moderna, el matemático alemán Carl Friedrich Gauss (1777-1885), quien quedó tan impresionado por su descubrimiento que lo llamó Theorema Egregium (teorema notable).
Javier Aramayona es científico titular en el Consejo Superior de Investigaciones Científicas y miembro del ICMAT.
Jeffrey F. Brock es decano de ciencias de la Facultad de Artes y Ciencias y decano de Ingeniería y Ciencia Aplicada en la Universidad de Yale (EE UU), donde ocupa la Cátedra Zhao and Ji de Matemáticas.
Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.