El alquerque

Al cortar una baraja de 52 cartas, en teoría podemos separar entre 0 y 51, ya que es posible el corte nulo o no-corte, que se suele indicar dando unos golpecitos con los dedos sobre el mazo (separar las 52 cartas equivale al corte nulo, ya que el mazo se queda como estaba). Y digo “en teoría” porque en la práctica nadie separa, por ejemplo, 1 carta o 51 (sería incluso difícil físicamente), y el corte suele situarse hacia la mitad del mazo, por lo que la probabilidad de formar dos montones iguales, pedida la semana pasada, es sustancialmente mayor que la probabilidad teórica, que es 1/52.

En cuanto a la probabilidad de que un montón sea el doble que el otro, mis sagaces lectoras/es se habrán dado cuenta de que es una pregunta trampa/broma: 52 no es divisible por tres, y, por tanto, la probabilidad es 0. Pero si el que reparte es Ace in the Sleeve Morgan, que una de cada dos veces se mete un as en la manga, la probabilidad de que haya solo 51 cartas es 1/2, y en ese caso se puede conseguir que un montón sea el doble del otro separando 17 o 34 cartas; por lo tanto, la probabilidad pedida, si reparte Morgan, es 1/2 x 2/51 = 1/51 (huelga señalar que en este caso la probabilidad 0 es la de que haya dos montones iguales).

En cuanto a la probabilidad de que nos toque al menos un as en una mano de póker, se obtiene más fácilmente calculando la probabilidad contraria, es decir, la de que no nos toque ninguno. Puesto que cuatro de las 52 cartas son ases, la probabilidad de que la primera que nos dan no sea un as es 48/52, la de que tampoco lo sea la segunda es 47/51, la tercera 46/50, la cuarta 45/49 y la quinta 44/48; por lo tanto, la probabilidad de que ninguna sea un as es el producto de estas cinco fracciones: 35673/54145, y la de que salga alguno será la probabilidad complementaria: 1 – 35673/54145 = 18472/54145, aproximadamente 1/3. De modo que si a lo largo de una partida de póker no te sirven al menos un as un tercio de las veces, puede que estés jugando con Ace in the Sleeve Morgan.

Del alquerque a las damas

Del Grupo Alquerque de Sevilla, mencionado en las últimas semanas, no solo cabe señalar sus valiosas aportaciones a la didáctica de las matemáticas, sino también la acertada elección del nombre, pues el alquerque es un destacado ejemplo de la versatilidad y el potencial pedagógico de algunos juegos de tablero.

Según el número de fichas de cada bando, hay tres modalidades básicas: alquerque de tres (homologable al popular tres en raya), alquerque de nueve (homologable al molino) y alquerque de 12.

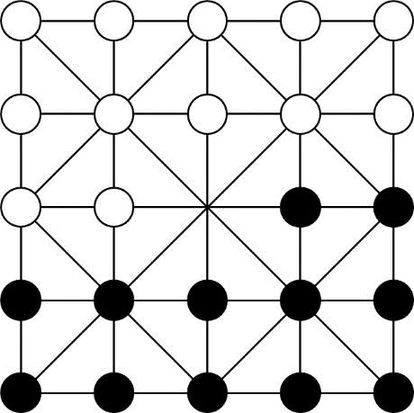
En la figura vemos la posición de partida del alquerque de 12. Los jugadores, por turno, llevan una de sus fichas a un punto de intersección vacío o, si pueden, “comen” una ficha contraria saltando sobre ella a un punto vacío. Gana quien captura todas las fichas contrarias o les impide mover. En el siglo XV, el alquerque de 12 se fusionó con el tablero de ajedrez y dio lugar a las damas. Invito a mis sagaces lectoras/es a llevar las 24 fichas del alquerque sobre el tablero de 8×8 manteniendo la estructura del juego. No sin antes calcular el número de jugadas posibles en el primer movimiento, en el segundo, en el tercero… ¿Se vislumbra alguna estrategia ganadora?

No solo las damas se derivan del alquerque, sino también otros juegos de tablero, como el molino (idéntico al alquerque de nueve en una de sus versiones), más conocido como Morris (o nueve hombres de Morris) en el mundo angloparlante. Pero se acaba el espacio-tiempo de la sección y habrá que dejarlo para la próxima entrega.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.