
Se nos dice que los computadores cuánticos ya están aquí y que son mucho más potentes que los convencionales. En particular, que en poco tiempo serán capaces de romper nuestras claves criptográficas. Muchos países están invirtiendo en esta tecnología para ser los primeros en alcanzar lo que se conoce como la “supremacía cuántica”. Pero, ¿sabemos cómo calcula un computador cuántico y cuál es la razón de esa potencia que se les atribuye?
Empecemos por la memoria. En un ordenador tradicional su unidad mínima es el bit, que puede contener un 0 o un 1. En un ordenador cuántico es el cúbit —abreviatura de bit cuántico— que puede contener un 0 o un 1, pero también cualquier combinación de esos dos estados básicos. Los físicos llaman a esta característica “superposición de estados” y nos dicen que eso es lo normal en el mundo de lo muy pequeño. Una partícula —tal como un protón— tiene, por ejemplo, una propiedad llamada “espín”, relacionada con sus propiedades magnéticas, que puede adoptar dos valores básicos llamados “arriba” y “abajo”, aunque lo habitual es que su estado sea una combinación de ambos. Podemos poner como analogía mundana de esta superposición un gin-tonic, el cual tendrá una cierta proporción de ginebra y otra de tónica. La información relevante que almacena el cúbit es el par de proporciones a y b de cada estado, es decir, dos números (para mayor precisión, se trata además de dos números complejos). Esto nos da ya una idea de la potencia de almacenamiento de un cúbit (cualquier proporción de ginebra y tónica) con respecto a la de un bit tradicional (solo ginebra, o solo tónica).
Otra característica del mundo físico es que los estados de dos partículas cuánticas pueden estar entrelazados, entendiendo por ello que están ligados entre sí. Esto nos permite construir memorias con varios cúbits entrelazados. De esa forma, dos cúbits estarían en una superposición de los cuatro estados básicos 00, 01, 10 y 11. Como consecuencia, dos cúbits almacenan cuatro números y, en general, n cúbits entrelazados almacenan 2Λn (2 elevado a n) números. Por ejemplo, en cinco bits las memorias tradicionales almacenan un solo número entero entre el 0 y el 31, pero cinco cúbits entrelazados almacenan 32 números complejos. Y ahí hay una ganancia exponencial.
Vayamos ahora con el cómputo: los cúbits operan entre sí mediante las llamadas “puertas cuánticas”. Por ejemplo, existe una puerta llamada X que, aplicada a un cúbit, convierte un 0 en un 1 y un 1 en un 0. Pero, esa puerta X es algo más compleja: aplicada a un cúbit con proporciones a y b de 0 y 1, pasa a un estado con proporciones b y a de 0 y 1. En nuestra analogía del gin-tonic, la puerta X intercambiaría las cantidades de ginebra y de tónica.
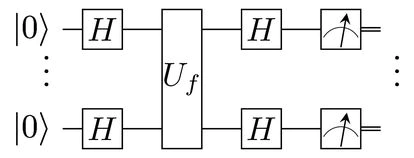
Al igual que hacemos con los circuitos de los ordenadores convencionales, enlazando varias puertas cuánticas se puede calcular una función compleja. Un algoritmo cuántico es, en esencia, un circuito formado por puertas cuánticas, que transforma el estado de un conjunto de cúbits desde una superposición inicial hasta otra final. ¿De dónde procede entonces su supuesta mayor potencia de cálculo?
Imaginemos una función implementada con puertas cuánticas, como, por ejemplo, la raíz cuadrada entera de un número. Supongamos que bastan n cúbits para contener el número de entrada. Mediante puertas cuánticas, es fácil conseguir que los n cúbits alcancen un estado que sea una superposición de todos los estados posibles de n bits. Siguiendo el ejemplo anterior, con cinco cúbits alcanzaríamos una superposición de 32 estados. Aquí es donde aparece la mayor potencia de los computadores cuánticos: el circuito cuántico calcularía la raíz cuadrada a la vez para los 32 valores posibles de la entrada y dejaría las 32 raíces cuadradas como una superposición en los cúbits de salida. Es decir, puede hacer en un solo paso lo que al ordenador convencional le costaría hasta 32 pasos realizar.
Pero, no todo es de color de rosa en el mundo cuántico porque este tiene algunos “caprichos”: las proporciones de la superposición —la proporción de ginebra y tónica— pertenecen a la “vida íntima” de las partículas cuánticas. Si un observador intenta medir el estado de los cúbits, su superposición se destruye. Es lo que sucede en la realidad física, aunque nadie sabe por qué: si se mide el espín de un protón, se destruye la superposición y el observador obtendrá uno de los dos estados, “arriba” o “abajo”, con cierta probabilidad cada uno, dependiendo de los valores de a y b. Es como si, al bebernos nuestro gin-tonic, se destruyera la mezcla que contiene y bebiéramos sólo ginebra o sólo tónica, sin poder anticipar cuál de las dos vamos a beber.
Los algoritmos cuánticos necesitan del ingenio humano para conseguir extraer más información a partir de la superposición de salida. Una forma habitual de proceder es hacer interferir los resultados calculados, unos con otros, mediante puertas cuánticas adicionales. Por ejemplo, podríamos calcular la suma o el producto de todos ellos o bien determinar cuántos de ellos son pares y cuántos impares. El más famoso de los algoritmos cuánticos, el que descompone un número entero en sus factores primos —debido al matemático Peter Shor, en 1994—, utiliza técnicas de este tipo.
Los algoritmos cuánticos ya están aquí. Ahora solo necesitamos computadores cuánticos con cientos de cúbits para ejecutarlos.
Ricardo Peña Marí es Catedrático Emérito de Lenguajes y Sistemas Informáticos de la Universidad Complutense de Madrid
Crónicas del Intangible es un espacio de divulgación sobre las ciencias de la computación, coordinado por la sociedad académica SISTEDES (Sociedad de Ingeniería de Software y de Tecnologías de Desarrollo de Software). El intangible es la parte no material de los sistemas informáticos (es decir, el software), y aquí se relatan su historia y su devenir. Los autores son profesores de las universidades españolas, coordinados por Ricardo Peña Marí (catedrático de la Universidad Complutense de Madrid) y Macario Polo Usaola (profesor titular de la Universidad de Castilla-La Mancha).
Para consultar las crónicas de otros años, haga clic aquí.
Puedes seguir a EL PAÍS TECNOLOGÍA en Facebook y Twitter o apuntarte aquí para recibir nuestra newsletter semanal.
