En su periplo peninsular de la semana pasada, si Papá Noel pudiera ir desde Madrid a cualquier otra de las comunidades autónomas tendría, en su primer desplazamiento, 14 posibilidades distintas, y desde cualquiera de ellas podría ir a cualquiera de las 13 restantes, y así sucesivamente, por lo que los itinerarios posibles serían 14 x 13 x 12… = 14! = 87.178.291.200; un número demasiado elevado, incluso para el superpoderoso Papá Noel, como para comparar entre sí todos los itinerarios en busca del más corto.
El número de itinerarios se reduce drásticamente si, como parece razonable, el trineo va desde cada comunidad a una de las limítrofes, lo que supone ir desde Madrid a una de las dos Castillas, y si Papá Noel elige Castilla-La Mancha luego tiene cinco posibilidades, y luego otras dos si eligiera Andalucía… El número de itinerarios sería 2 x 5 x 2…, muy por debajo del indiscriminado 14 x 13 x 12…
Pero Papá Noel podría reducir sus opciones a una, muy razonable, si desde cada comunidad viajara a la más próxima (de las aún no visitadas): de Madrid a Toledo, de Toledo a Mérida, de Mérida a Sevilla… De este modo estaría aplicando un “algoritmo voraz”.
En ciencias de la computación, un algoritmo voraz (también conocido como glotón, ávido, devorador o greedy) es una estrategia de búsqueda que consiste en elegir la mejor opción en cada paso del proceso con la esperanza de obtener la mejor solución global. Los algoritmos voraces se utilizan generalmente para resolver problemas de optimización, y las decisiones se toman en función de la información -o la valoración- que se maneja en cada momento. Suelen ser rápidos y fáciles de utilizar, pero no siempre llevan a la solución óptima.
Por ejemplo, en el caso que nos ocupa, el algoritmo voraz le ofrece a Papá Noel un buen itinerario, pero no el mejor (es decir, el más corto), pues el criterio de ir de cada comunidad a la más próxima lo llevaría de Valencia a Zaragoza, cuando una solución mejor sería ir antes a Barcelona para seguir el circuito esquematizado en la figura.
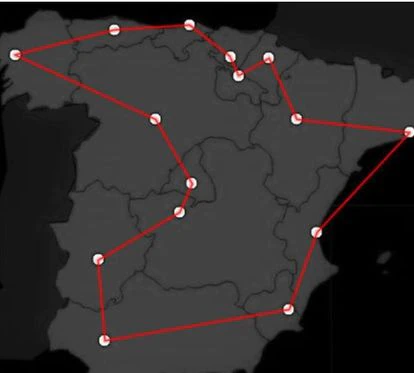
Por cierto, a mis sagaces lectoras/es no se les habrá escapado que el circuito más corto parece ser, paradójicamente, el que encierra una superficie mayor. ¿Es realmente así? ¿Por qué?
Para este itinerario -o cualquier otro- el tiro del trineo puede formarse, de forma que detrás de Rudolph vayan cuatro parejas heterosexuales, de 9.216 maneras distintas (4! x 4! x 2⁴).
Un saltamontes y dos sucesiones
Y de los renos voladores a los saltamontes invisibles, pues en la sección de comentarios de la semana pasada se mencionó un interesante problema que sigue sin resolver en el momento de escribir estas líneas:
Hay un saltamontes invisible en un punto entero de la recta real. El saltamontes se desplaza a saltos o bien a derecha o bien a izquierda, una cantidad entera cada segundo. Podemos intentar “cazar” al saltamontes situándonos cada segundo en un punto entero de la recta. ¿Hay alguna estrategia que nos permita cazar tarde o temprano al saltamontes invisible?
Y puesto que estrenamos nuevo año, no está de más echarle una ojeada al número 2022. ¿Detectan en él alguna propiedad interesante mis sagaces lectoras/es?
Y un par de sencillas sucesiones para terminar el año sin esforzarse demasiado:
2000, 2002, 2020, 2022…
62, 138, 262, 446…
¿Cuáles son los siguientes números?
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
