Nos preguntábamos la semana pasada cómo se puede repartir una tarta (o cualquier otra cosa) entre tres personas de forma que las tres den por bueno el reparto. En el caso de dos personas es muy sencillo, y además es una situación que se da a menudo en la vida real, cuando, por ejemplo, dos niños tienen que repartirse una chocolatina o un bocata: uno hace la partición y el otro elige, con lo que el primero pondrá buen cuidado en lograr que las dos partes sean iguales. Pero en el caso de tres personas -a las que llamaremos A, B y C- la cuestión se complica bastante. Una de las posibles soluciones (no es única, e invito a mis sagaces lectoras/es a buscar otras) es la siguiente:
A divide la tarta en tres partes, B elige dos y la que queda es para A. Si B considera que las dos partes que ha elegido son equivalentes, le da a elegir a C entre ambas y se queda con la restante (aunque C también tiene la opción de escoger la parte de A). Si B considera que los dos trozos que ha elegido no son iguales, corta una parte de uno de ellos para igualarlos antes de ofrecérselos a C; en este caso queda un trozo residual que los tres pueden repartirse de la misma manera: uno de ellos (no tiene por qué ser otra vez A) lo divide en tres partes, etc. Teóricamente, el proceso podría repetirse ad infinitum (o hasta alcanzar el nivel molecular); pero en la práctica no suele ser necesario pasar del primer paso, a no ser que la tripartición de A sea claramente inequitativa.
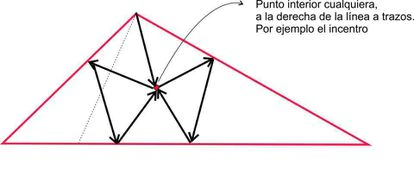
En cuanto a la división de un triángulo obtusángulo en acutángulos, la condición innecesaria que se suele autoimponer la gente al intentar resolverlo es la de que todos los acutángulos tengan todos sus vértices sobre los lados del obtusángulo, y de este modo es imposible; pero, como se puede ver en el dibujo enviado por Enol Ferre, la partición es posible haciendo coincidir varios vértices de los acutángulos en un punto interior del obtusángulo. ¿Es mínima esta división en siete acutángulos? (Obsérvese, dicho sea de paso, el paralelismo “psicológico” con el famoso problema de los nueve puntos a unir con cuatro trazos rectilíneos).
Partición de un número natural
Y puesto que hemos hablado de partir y repartir, es obligado mencionar el concepto matemático de partición de un número natural, que consiste en descomponerlo en la suma de otros números naturales (es decir, enteros y positivos).
El de las particiones es uno de esos fascinantes temas matemáticos que, a partir de un planteamiento extremadamente simple, cuya comprensión y primeros desarrollos están al alcance de cualquiera, abre un campo de ilimitadas posibilidades e innumerables aplicaciones.
Veamos las particiones de los primeros números naturales:
El 1 no puede descomponerse en sumandos, por lo que solo tiene una partición (el número mismo se considera una de sus particiones).
El 2 se puede descomponer en sumandos de una sola manera: 2 = 1 + 1 y, por tanto, tiene dos particiones.
El 3 tiene tres particiones 3 = 2 + 1 = 1 + 1 + 1.
El 4 tiene cinco particiones: 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1.
El 5 tiene siete particiones…
El matemático británico Alfred Young (1873-1940) ideó los diagramas que llevan su nombre para visualizar las particiones:

Invito a mis sagaces lectores a interpretar los diagramas de Young, a relacionarlos con otro asunto tratado hace unos meses en esta misma sección, a construir la secuencia del número de particiones de los sucesivos números naturales y a sacar las conclusiones pertinentes.
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal